Frequency Comb - Spaceborne Frequency Comb Metrology
EO
Atmosphere
Mission complete
DLR
Quick facts
Overview
| Mission type | EO |
| Agency | DLR |
| Mission status | Mission complete |
| Launch date | 16 Apr 2015 |
| End of life date | 16 Apr 2020 |
| Measurement domain | Atmosphere, Gravity and Magnetic Fields |
| Measurement category | Gravity, Magnetic and Geodynamic measurements, Ozone |
| Measurement detailed | Atmospheric stability index |
| Instruments | Laser Reflectors, Passive Synthetic Aperture Radar |
| Instrument type | Other, Atmospheric chemistry, Data collection, Gravity instruments |
| CEOS EO Handbook | See Frequency Comb - Spaceborne Frequency Comb Metrology summary |
Frequency Comb - Spaceborne Frequency Comb Metrology
Overview Prototype Experiment Results References
Precision time references are of major importance to spaceborne missions, such as global satellite navigation, Earth observation, satellite formation flying and fundamental science experiments. An optical "frequency comb" is a very precise tool for measuring different colors—or frequencies—of light. The technology, made possible by recent advances in ultrafast lasers, can accurately measure much higher frequencies than any other tool. 1)
The company Menlo Systems GmbH of Martinsried near Munich, in collaboration with several institutes in Germany, as well as funding from DLR (German Aerospace Center) and the EC (European Commission), has demonstrated a reproducible spaceborne optical atomic transition frequency system, making use of a compact and remotely controllable comb setup referenced to a cesium clock. The experiment on a sounding rocket flight campaign compared two clocks, one based on the optical D2 transition in Rb, and another on hyperfine splitting in Cs. This represents the first frequency comb based optical clock operation in space, which is an important milestone for future spaceborne precision metrology. 2) 3)
The objective of the prototype experiment involved microgravity on a sounding rocket flight for a duration of 6 minutes. With respect to LPI (Local Position Invariance), a cornerstone of general relativity, the apparent experimental limitations are caused by the reference clock, the selected Rb transition monitored using frequency modulation spectroscopy, and the limited variation in the gravitational potential during this flight.
Background
The upcoming generation of optical atomic frequency references has shown an enormous increase in accuracy and stability compared to the present official atomic clock standard based on Cesium. These amazingly stable optical atomic clocks are based on energy transitions that have been carefully quantum engineered and controlled, and that are oscillating at frequencies of several hundred THz ( terahertz) with a stability of 10-18. Optical clocks have, for example, demonstrated a precision that is sensitive enough to detect a few centimeters of elevation change within the Earth's gravitational potential, caused by the relativistic redshift.
In addition, the recent discovery of gravitational waves has triggered a growing interest in their advanced detection. 4) Gravitational wave detectors are large Michelson interferometers that compare optical phases of a stable laser sent via the two orthogonal arms. Typical laser linewidths are ~10 Hz, and a strain sensitivity approaching 10-23 √Hz-1 has been reported . 5) Advanced gravitational wave detectors like LISA, which are designed as very large baseline interferometers between satellites, have been a long-lasting dream of the scientific community. 6) Such a space-based device would be important for the detection of low-frequency waves (<1 Hz).
Whenever it comes to the calibration and stabilization of lasers used for such precision metrology, it is often necessary to divide their optical frequency with an optical clockwork into a countable radio frequency, so that they can be referenced to an SI frequency standard. The established method of choice for this frequency division is using an optical frequency comb. Since its invention, 7) the frequency comb has enabled various fundamental experiments and paved the way to groundbreaking applications, ranging from precision astronomy, femtosecond precision time transfer, nanometer ranging, fundamental physics, and gravimetry to laser stabilization and cooling. Apart from the work of Sinclair et al. ,8) however, the operation of combs has been limited to research laboratories providing well-controlled environmental conditions. For many reasons there exists fundamental interest in applying precision laser metrology and optical clocks in space. In this environment, an optically referenced comb with ultimate performance in terms of phase noise and stability could be used to investigate general relativity, provide low-noise microwaves for synthetic aperture radar, calibrate lidar lasers for an in-depth study of the planetary atmosphere, improve on global satellite navigation systems, enable fast precision inter-satellite laser ranging systems for swarm navigation, and transfer time and frequency over large grids with femtosecond jitter. 9)
Prototype Experiment
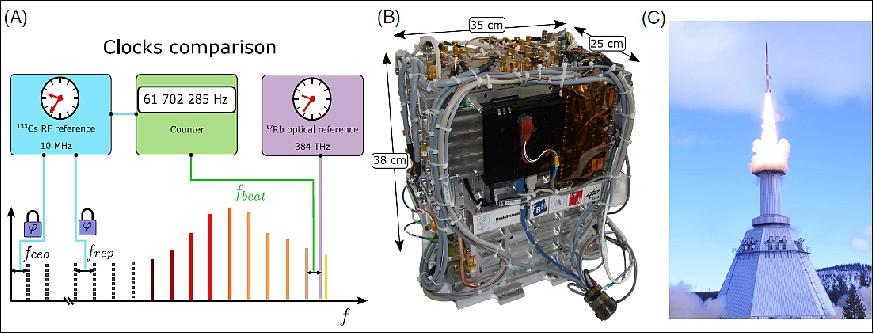
The goal was to demonstrate that optical frequency combs referencing a selected optical atomic line to a radio frequency clock can be scaled down to a module with a volume below 20 l (liter), having a mass of 22 kg, and operating under the conditions of a sounding rocket flight. An illustration of the experiment, where the 87Rb D2 transition at 384 THz to a 10 MHz Cs-based atomic reference is compared, is shown in Figure 1(A). The assembled module is depicted in Figure 1(B). Taking into account the actual flight data and currently ongoing developments, future satellite applications become well within reach. Low-bandwidth remote operation with a high degree of automation and environmental stability against accelerations >10 g or shocks are demonstrated here. Precision thermal stabilization of the comb module with stabilities within ±30 mK in a convection-limited microgravity environment has been achieved.
Essentially, optical frequency combs are precision-controlled femtosecond lasers. Phase-locked loops lock two radio frequencies, the pulse repetition rate f rep and the carrier envelope offset frequency f ceo of them. An optical spectrum is then generated with evenly spaced lines, following the comb equation f c = f ceo + n x f rep (with n being a natural number). Usually, such lasers are mechanically sensitive to vibrations and temperature variations. This environmental sensitivity can be reduced using polarization-maintaining fibers.
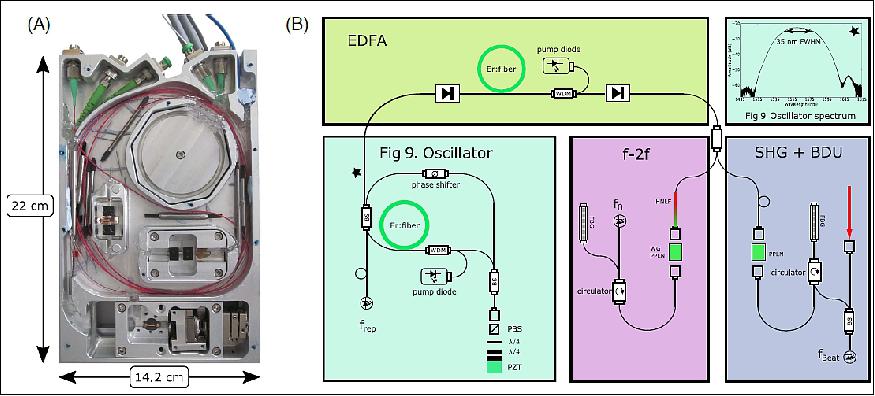
The frequency comb laser is based on a nonlinear amplified loop mirror, with erbium as the gain medium. A recent comparative study has pointed out the superior performance of this technology. The complete f rep = 100 MHz comb fits into a small package of 220 mm x 142 mm x 25 mm (Figure 2), including the laser oscillator, erbium-doped fiber amplifier (EDFA), ridge waveguide (WG) periodically poled lithium niobate (PPLN) based f –2f interferometer, and, for Rb optical beat generation at 780 nm, a 1560 nm PPLN second-harmonic generation (SHG) unit. The module has a mass of 1.65 kg, mostly due to the aluminum body, which also serves as a thermal mass. Efficient heat transport under microgravity was ensured by embedding the fiber components in space-grade silicon rubber (NUSIL CV-2500).
The comb receives 780 nm light from the atomic spectroscopy unit consisting of a micro-integrated and space-qualified diode laser locked to a Doppler-free Rb spectroscopy cell. The size of this module is 220 mm x 142 mm x 50 mm, with a total mass of 2.1 kg. The diode laser is a ridge waveguide DFB (Distributed Feedback) diode laser with a cavity length of 1.5 mm, shown in Figure 3(A). It is mounted on aluminum nitride, omitting any movable parts, including an optical micro-isolator with 60 dB isolation and a fiber coupler connecting the laser to the miniature Rb spectroscopy unit, shown in Figure 3(B). The DFB laser emits 10 mW at 780 nm behind the micro-isolator and is continuously tunable over 0.7 nm via injection current control with a side mode suppression ratio of >50 dB at 10 pm resolution bandwidth. A short term laser linewidth (10 µs) of 1 MHz FWHM and a white noise floor based Lorentzian linewidth of 66 kHz has been observed. The Doppler-free spectroscopy for frequency stabilization of the DFB laser has been realized in a miniaturized optics unit situated on a Zerodur bench. The Rb transition selected for the observation is the D2 transition from the 52S1/2 ground state to the 52P3/2 excited state. Using Doppler-free saturation spectroscopy absorption lines on the order of the natural linewidth of Rb (6 MHz) can be addressed. Frequency modulation of the DFB laser is used for locking, shown schematically in Figure 3(C).
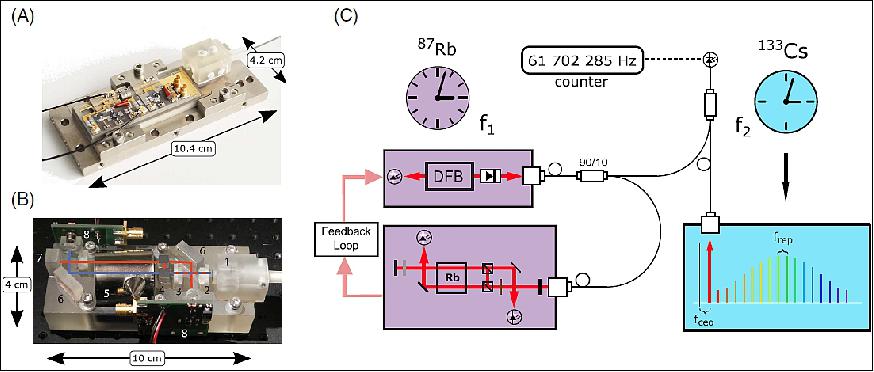
The complete optics module is controlled by a compact mixed-signal electronics unit (170 mm x 197 mm x 310 mm, 12 kg). The collected data are streamed to a pocket-sized microcomputer used for high-level data processing and interfacing to ground station equipment. Radio electronics and phase locks were referenced to a miniature CSAC (Chip-Scale Atomic Clock; Microsemi). Repetition rate, offset beat, and Rb beat are monitored using an advanced multichannel synchronous digital phase recording and counting system (K&K GmbH).
During the microgravity mission it was possible to observe and control the experiment from the ground station equipment via a 9.6 kbaud radio link. The complete assembly, as shown in Figure 1(B) with a size of 310 mm x 200 mm x 480 mm, was integrated into an airtight vessel and pressurized to 1200 mbar to preserve constant pressure conditions during the space flight. During flight, the pressure inside the vessel changed slowly by 1.6% due to an overall temperature increase of 2°C caused by heat dissipation of the device. The thermal load of the module is dumped into the baseplate of the vessel with five heatpipes and direct mechanical contact. Until 10 s before launch, the baseplate is water cooled to 15°C with a thermoelectric chiller situated within the launch tower and connected to the payload with two removable hoses. Before launch the module was environmentally tested on a shaker table and in a climate chamber, which ensured full compliance with the expected rocket launch and reentry conditions.
Results
So far, two successful flights on sounding rockets have been performed with TEXUS 51 on April 23, 2015 and TEXUS 53 on January 23, 2016, both launched from the ESRANGE Space Center in northern Sweden.
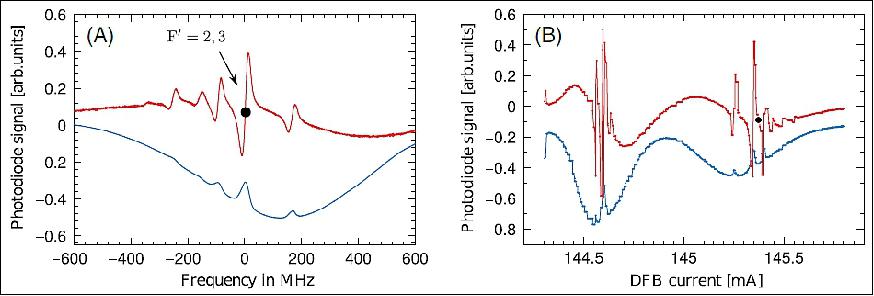
The description is concentrated on on the flight data of TEXUS 51, because the clock comparison data for TEXUS 53 was affected by a thermally dependent etalon in the Rb spectroscopy module, which would require advanced numerical treatment of the data to be further considered. About 5 h before launch, the unit was powered and allowed to thermalize. Comb and Rb spectroscopy were locked and ground station data were acquired for reference. At g = 9.81 ms-2 the selected Rb D2 line was determined to be 384.2279817(4) THz. A laser spectroscopy scan at ground is shown in Figure 4(A). 10 s before rocket launch the system was switched into a secure state: while the Rb spectroscopy remained locked to the atomic line, the comb was unlocked in repetition rate and offset frequency to relax the servo actuators. The servo bandwidth and actuator strength are insufficient to cope with the accelerations during launch.
Launch time t0 was followed by vertical accelerations reaching 12.5 g. The Rb spectroscopy unit stayed locked during such accelerations, and the comb oscillator remained mode locked. After motor separation, just before the beginning of the microgravity phase, the two servo locks of the comb were turned on and a lock of f rep was reached within seconds. For TEXUS 51, the microgravity regime (<10-4 g for all directions) started at t0+72 s, and the carrier offset frequency f ceo was locked at t0+84 s.
Such fast relocking of the comb was also achieved on the TEXUS 53 flight. The Rb beat note with the nearest comb line was counted until t0 + 330 s [Figure 5(B)]. Then, for 120 s, a wavelength scan was initiated, resulting in the spectroscopy data shown in Figure 4(B). To keep the duration of this scan short enough, a larger current step size was used compared to the precision scan in Figure 4(A). From t0 + 450 s on, the laser was locked again to the Rb line for 30 s. The microgravity phase ended at t0 + 442 s, directly followed by reentry into Earth's atmosphere. During reentry, under decelerations of up to 12.5 g, the comb unit lost its phase locks, but the laser remained mode locked. The DFB laser module stayed locked to the Rb D2 transition during both flights for the full flight period. Touchdown of the unpowered payload occurred at t0 + 884 s. The payload was recovered within a few hours and disassembled the same day. The comb module's functionality was positively assured within 24 h after return to ground.
The absolute clock comparison accuracy is limited by long-term drifts of the references, e.g., fluctuations of the locking point of the Rb laser, drifts of the CSAC, and some uncertainties due to light shift and Zeeman shift. Figure 5(A) shows a long-term dataset from the ground. The systematic limits of our clock comparison are discussed in more detail in Section 4 of Supplement 1. However, for the relevant time scales below 1000 s, a relative frequency change can be measured with a precision approaching 10-11 at 100 s. Figure 5(B) shows the relative change in frequencies throughout the TEXUS 51 flight, including the data taken immediately before launch, at payload apogee, and immediately before reentry into the atmosphere. A linear drift of 122 Hz/s, which was caused by a slight thermal drift within the spectroscopy module, has been subtracted from the flight data.
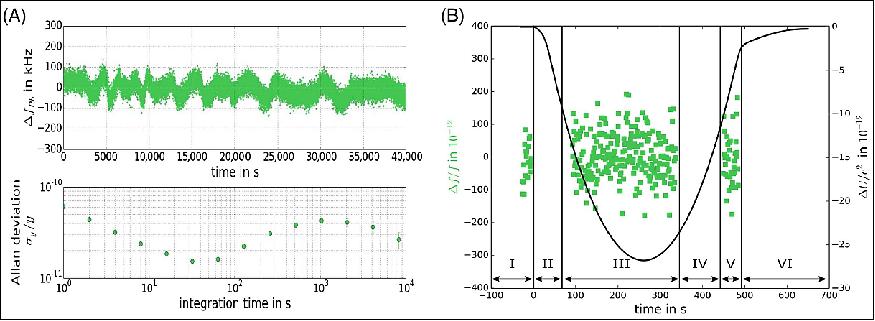
The clock comparison experiment can be evaluated with respect to the LOI (Local Position Invariance), a cornerstone of general relativity, as it is one of the three postulates of Einstein's equivalence principle. If two different types of clocks are operating at different frequencies f 1 and f 2, they can be compared in varying gravitational potentials ΔU, leading to (f 1 - f 2) /f =(β1 - β2) ΔU/c2, where βi are dimensionless parameters depending on the sensitivity of each clock on LPI.
Present clock comparisons on Earth have determined that Δβ = β1 - β2 < 10-6. Taking into account recent clock accuracies reaching 10-18, largely improved earthbound measurements are fundamentally limited by the gravitational variation given by the Earth's trajectory in the solar system. Performing a least squares analysis of the observed optical frequency during the sounding rocket flight and comparing it to the gravity potential dataset, as shown in Figure 5(B), we evaluate Δβ < 0.19 ± 0.26. While we acknowledge that the present result is 5 orders of magnitude less precise than state of the art based determinations of Δβ on Earth, we note that neither the measurement principle nor the frequency comb is limiting us. For example, by choosing an advanced space-compatible RF reference like PHARAO (Project d'Horloge Atomique à Refroidissement d'Atomes en Orbite) and an optical clock based on Yb, Sr, Al, or I2, a frequency comb-based comparison on the level of 10-15 or beyond is feasible with a space comb on a satellite.
Menlo Systems has recently demonstrated an ultra-low noise comb performance with an Allan deviation better than 10-16 at 1 s, dropping below 10-18 within 500 s. Apart from additional low-voltage-driven electrooptical actuators in the oscillator and advanced high-bandwidth phase-locked loops, the fiber design of such a comb is very comparable and fits into a similar volume to that presented here. Such an instrument, on a trajectory passing through a gravitational potential difference ΔU = 1010 m2s-2 (i.e., from Earth to Mercury), could allow for the determination of Δβ down to a level of 10-9, thereby improving present Earth-bound experiments by 3 orders of magnitude.
In conclusion, we have reproducibly demonstrated spaceborne determination of an optical atomic transition frequency, making use of a compact and remotely controllable comb setup referenced to a cesium clock. The prototype experiment involved microgravity on a sounding rocket flight for a duration of 360 s. With respect to LPI, the apparent experimental limitations are caused by the reference clock, the selected Rb transition monitored using frequency modulation spectroscopy, and the limited variation in the gravitational potential during this flight. Nevertheless, with our prototype experiment, the technology readiness of optical frequency combs and remotely controlled precision laser spectroscopy has been significantly advanced.
It is pointed out that the current weight and volume of the module can be further optimized. Most of the current mass is caused by the structure itself. Most of the current mass is caused by the structure itself. Moreover, in the future, the application of advanced atomic spectroscopy techniques like modulation transfer spectroscopy, combined with cavity enhancement, is feasible. We note that such devices have been recently designed for space use. 10) Such a spectroscopy setup could already improve the optical clock by 4 orders of magnitude to a stability of 10-15. Finally, the electronics package can be improved while reducing the number of modules, power consumption, and performance and interface complexity. The next generation of the space comb setup with a significantly reduced mass below 10 kg, an overall power consumption below 30 W, and an improved spectroscopy module is currently under development and has been scheduled for a rocket launch in 2017. This next-generation system will also be tested for operation under vacuum conditions, and, moreover, some critical fiber components will be more deeply inspected for radiation hardness. Based on our technology, we expect a promising future for various comb applications in space. Space combs could largely serve for clocks and frequency standards, microwave generation, ranging, and laser calibration out there.
References
1) "Optical Frequency Combs," Menlo Systems, URL: http://www.menlosystems.com/assets/documents-2/Optical-Frequency-Combs.pdf
2) Matthias Lezius, Tobias Wilken, Christian Deutsch, Michele Giunta, Olaf Mandel, Andy Thaller, Vladimir Schkolnik, Max Schiemangk, Aline Dinkelaker, Anja Kohfeldt, Andreas Wicht, Markus Krutzik, Achim Peters, Ortwin Hellmig, Hannes Duncker, Klaus Segstock, Partick Windpassinger, Kai Lampmann, Thomas Hülsing, Theodor W. Hänsch, Ronald Holzwarth, "Spaceborne Frequency Comb Metrology," Optica, Vol. 3, No 12, pp: 1380-1387, Dec. 2016, DOI: 10.1364/optica.3.001380, URL: https://www.osapublishing.org/DirectPDFAccess/DBE99771-B99B-C7D3-BC1981AC3BB40F6B-354726/optica-3-12-1381.pdf?da=1&id=354726-&seq=0&mobile=no
3) "Spaceborne frequency comb metrology: supplement material, Supplement 1," URL: https://www.osapublishing.org/DirectPDFAccess/0CB4BDDA-CCEE-4C09-15D0A068B5C5E2C7_354726/optica-3-12-1381.PDF?da=1&id=354726&seq=1&mobile=no
4) B. P. Abbott, R. Abbott1 T. D. Abbott, M. R. Abernathy, et al., LIGO Scientific Collaboration and Virgo Collaboration, "Observation of Gravitational Waves from a Binary Black Hole Merger," Physical Review Letters, Vol. 116, Feb. 12, 2016, DOI: 10.1103/PhysRevLett.116.061102, URL: https://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.116.061102
5) D. V. Martynov, E. D. Hall, et al., "Sensitivity of the Advanced LIGO detectors at the beginning of gravitational wave astronomy," Physical Review D, Vol. 93, Issue 11, June 1, 2016, URL: https://arxiv.org/pdf/1604.00439v2.pdf
6) K Danzmann for the LISA Study Team, "LISA - an ESA cornerstone mission for a gravitational wave observatory," Classical and Quantum Gravity, Volume 14, No 6, pp: 1399-1004, 1997
7) R. Holzwarth, Th. Udem, T. W. Hänsch, J. C. Knight, W. J. Wadsworth, P. St. J. Russell, "Optical Frequency Synthesizer for Precision Spectroscopy," Physical Review Letters, Vl. 85, No 11, Sept. 11, 2000, URL: https://www.aps.org/newsroom/pressreleases/upload/hansch.pdf
8) L. C. Sinclair, I. Coddington, W. C. Swann, G. B. Rieker, A. Hati, K. Iwakuni, N. R. Newbury, "Operation of an optically coherent frequency comb outside the metrology lab," Opt. Express Vol. 22, Issue 6, pp: 6996–7006, 2014, URL: https://www.osapublishing.org/DirectPDFAccess/E4218956-F8F2-7412-803CED4086CE9D33-281995/oe-22-6-6996.pdf?da=1&id=281995&seq=0&mobile=no
9) Fabrizio R. Giorgetta, William C. Swann, Laura C. Sinclair, Esther Baumann, Ian Coddington, Nathan R. Newbury, "Optical two-way time and frequency transfer over free space," Nature Photonics, Vol. 7, pp: 434–438, April 2013, doi:10.1038/nphoton.2013.69, URL: http://ws680.nist.gov/publication/get_pdf.cfm?pub_id=912449
10) Thilo Schuldt, Klaus Döringshoff, Alexander Milke, Josep Sanjuan, Martin Gohlke, Evgeny V. Kovalchuk, Norman Gürlebeck, Achim Peters, Claus Braxmaier, "High-Performance Optical Frequency References for Space," 8th Symposium on Frequency Standards and Metrology 2015, Journal of Physics, Conference Series, Volume 723, 2016, 012047, doi:10.1088/1742-6596/723/1/012047, URL: http://iopscience.iop.org/article/10.1088/1742-6596/723/1/012047/pdf
The information compiled and edited in this article was provided by Herbert J. Kramer from his documentation of: "Observation of the Earth and Its Environment: Survey of Missions and Sensors" (Springer Verlag) as well as many other sources after the publication of the 4th edition in 2002. - Comments and corrections to this article are always welcome for further updates (eoportal@symbios.space).